**Tile Painting: Revisited!

Tile Painting: Revisited!

Nikita just came up with a new array game. The rules are as follows:

• Initially, there is an array, A$A$, containing N$N$ integers.
• In each move, Nikita must partition the array into 2$2$ non-empty parts such that the sum of the elements in the left partition is equal to the sum of the elements in the right partition. If Nikita can make such a move, she gets 1$1$ point; otherwise, the game ends.
• After each successful move, Nikita discards either the left partition or the right partition and continues playing by using the remaining partition as array A$A$.

Nikita loves this game and wants your help getting the best score possible. Given A$A$, can you find and print the maximum number of points she can score?

Input Format

The first line contains an integer, T$T$, denoting the number of test cases. Each test case is described over 2$2$lines in the following format:

1. A line containing a single integer, N$N$, denoting the size of array A$A$.
2. A line of N$N$ space-separated integers describing the elements in array A$A$.

Constraints

• 1≤T≤10$1\le T\le 10$
• 1≤N≤214$1\le N\le 2^{14}$
• 0≤Ai≤109$0\le A_i\le {10}^9$

Scoring

• 1≤N≤28$1\le N\le 2^8$ for 30%$30\mathrm{\%}$ of the test data
• 1≤N≤211$1\le N\le 2^{11}$ for 60%$60\mathrm{\%}$ of the test data
• 1≤N≤214$1\le N\le 2^{14}$ for 100%$100\mathrm{\%}$ of the test data

Output Format

For each test case, print Nikita's maximum possible score on a new line.

Sample Input

3
3
3 3 3
4
2 2 2 2
7
4 1 0 1 1 0 1

Sample Output

0
2
3

Explanation

Test Case 0:

Nikita cannot partition A$A$ into 2$2$ parts having equal sums. Therefore, her maximum possible score is 0$0$and we print 0$0$ on a new line.

Test Case 1:

Initially, A$A$ looks like this:

She splits the array into 2$2$ partitions having equal sums, and then discards the left partition:

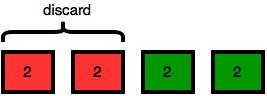
She then splits the new array into 2$2$ partitions having equal sums, and then discards the left partition:

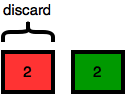
At this point the array only has 1$1$ element and can no longer be partitioned, so the game ends. Because Nikita successfully split the array twice, she gets 2$2$ points and we print 2$2$ on a new line.

------------------------------------------------EDITORIAL------------------------------------------

Solution

This problem can be solved using straightforward dynamic programming. Let's maintain a DP[N][N]table where an entry DP[L][R] denotes the maximum points we can score by playing the game on a subarray from L to R.

We can fill up the DP table in O(N3)$O(N^3)$ using following recursive recurrence:

• DPL,R=max(DPL,R,max(DPL,X,DPX+1,R)+1)$D{P}_{L,R}=max(D{P}_{L,R},max(D{P}_{L,X},D{P}_{X+1,R})+1)$ if ∑L≤i≤XAi=∑X<i≤RAi$\sum _{\begin{array}{c}L\le i\le X\end{array}}{A}_i=\sum _{\begin{array}{c}X<i\le R\end{array}}{A}_i$
• DPL,R=0$D{P}_{L,R}=0$ if there is no such X$X$.

C++ Code:
Language : C++

const int maxn = 2048 + 10;
int dp[ maxn ][ maxn ], n;
long long int A[ maxn ];

long long int sum(int l, int r) {
    return A[r] - A[l-1];
}

int solve(int l, int r) {
    int &ret = dp[l][r];
    if( ret != -1 ) return ret;
    ret = 0;
    for(int x=l; x<r; x++) {
        if(sum(l, x) == sum(x+1, r)) // valid x
            ret = max(ret, max(solve(l, x), solve(x+1, r)) + 1);
    }
    return ret;
}

int main() {
    int t; cin >> t;
    while( t-- ) {
        int n; cin >> n;
        for(int i=1; i<=n; i++) {
            cin >> A[i];
            A[i] += A[i-1];
        }
        memset(dp, -1, sizeof dp);
        cout << solve(1, n) << "\n";
    }
    return 0;
}

Careful observation reduces the complexity to O(N2)$O(N^2)$. It should be noted that maximum points for a subarray can be calculated by considering only the first valid X$X$ for a subarray (rather than by considering all valid X$X$).

Steps Involved:

• Find first valid X$X$ for all subarrays.
• Populate DP as shown above but by considering only first valid X$X$.

C++ code:

Language : C++

const int maxn = 2048 + 10;
int n; 
long long int A[ maxn ];
int L[ maxn ][ maxn ], dp[ maxn ][ maxn ];

int solve(int l, int r) {
    if( l > r ) return 0;
    if( L[l][r] == -1 ) return 0;
    int &ret = dp[l][r];
    if( ret != -1 ) return ret;
    ret = 0;
    ret = max(ret, max(solve(l, L[l][r]), solve(L[l][r]+1, r)) + 1);
    return ret;  
}

int main() {
    int t; cin >> t;
    while( t-- ) {
        int n; cin >> n;
        for(int i=1; i<=n; i++) {
            cin >> A[i];
            A[i] += A[i-1];
        }

        for(int i=1; i<=n; i++) {
            for(int j=i; j<=n; j++) {
                L[i][j] = -1; // to store first valid X
                dp[i][j] = -1; // to store maximum points
            }
        }

        // finding first valid X for each subarray
        for(int i=1; i<=n; i++) {
            long long int s = 0;
            int l = i;
            for(int j=i; j<=n; j++) {
                s += A[j] - A[j-1];
                if( s % 2 == 0 ) {
                    s /= 2;
                    while( l < j && A[l]-A[i-1] < s) l++;
                    if( l < j && A[l]-A[i-1] == s ) L[i][j] = l;
                    s *= 2;
                }
            }
        }
        cout << solve(1, n) << "\n";
    }
    return 0;
}

We can optimize the above solution to work in O(Nlog(N))$O(Nlog(N))$ using binary search. Find the first valid X$X$in the range [L,R]$[L,R]$ using binary search, then divide the range into 2$2$ parts (i.e.: [L,X] & [X+1,R]$[L,X]\mathrm{\&}[X+1,R]$), compute the answer for both parts recursively and then take the maximum answer from both parts to compute the answer of range [L,R]$[L,R]$. This can be implemented as follows:

C ++ Code:

long long a[100010];

ll sum(int l, int r) {
    return a[r] - a[l-1];
}

// binary search to find first valid X
// within subarray [l, r]
int get(int l, int r, ll s) {
    int low, high, mid;
    low = l;
    high = r;
    while( low <= high ) {
        mid = ( low + high ) / 2;
        ll x = sum(l, mid);
        if( x == s && (mid == l || sum(l, mid-1) != s )) {
            return mid;
        } else if( x >= s ) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return -1;
}

int solve(int l,int r){
    ll s = sum(l, r);
    if( l != r && s % 2 == 0 ) {
        int ind = get(l, r, s/2);
        if( ind != -1 ) {
            // compute maximum from 2 parts 
            return max(solve(l, ind), solve(ind+1, r)) + 1;
        }
    }
    return 0;
}

int main() {
    int t;
    cin>>t;
    while (t--){
        int n;
        cin>>n;
        assert(n <= 16384);
        for (int i=1;i<=n;i++) {
            cin>>a[i];
            a[i]+=a[i-1];
        }
        cout<<solve(1,n)<<endl;
    }
    return 0;
}

/ MY CODE

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
#define ff first
#define ss second
#define mp make_pair
#define pb push_back
  int n;
lli arr[162390];
int solve(int l,int r,lli ms)
 {
          if(l>=r) return 0;
          if(r>=n) return 0;
         int  ci=l;
         lli cs=0;
         int f=1;
         while((cs<ms/2 || f==1) && ci<=r)
             {
               
                f=0;
                   cs+=arr[ci];
                   ci++;
                
    }
    if(cs==ms/2  && ms%2!=1)
     {
      return max(solve(l,ci-1,ms/2),solve(ci,r,ms/2))+1;
     }
     else return 0;
    
 }
int main()
{
  
//  freopen("abc.txt","r",stdin);
//  freopen("pqr.txt","w",stdout);
  int t;
   cin>>t;
   while(t--)
   {
      //cout<<"bacl";
    scanf("%d",&n);
      lli sum=0;
      for(int i=0;i<n;i++)
         {
          scanf("%lld",&arr[i]);
         sum+=arr[i];
    }
    if(sum%2==1)
    {
       cout<<0<<endl;
    }
    else
    cout<<solve(0,n-1,sum)<<endl;
    
   }
}

 Set by ma5termind

Problem Setter's code :

#include <bits/stdc++.h>
using namespace std;

#define ll long long int

long long a[100010];

ll sum(int l, int r) {
    return a[r] - a[l-1];
}

int get(int l, int r, ll s) {
    int low, high, mid;
    low = l;
    high = r;
    while( low <= high ) {
        mid = ( low + high ) / 2;
        ll x = sum(l, mid);
        if( x == s && (mid == l || sum(l, mid-1) != s )) {
            return mid;
        } else if( x >= s ) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return -1;
}

int solve(int l,int r){
    ll s = sum(l, r);
    if( l != r && s % 2 == 0 ) {
        int ind = get(l, r, s/2);
        if( ind != -1 ) {
            return max(solve(l, ind), solve(ind+1, r)) + 1;
        }
    }
    return 0;
}

int main() {
    int t;
    cin>>t;
    while (t--){
        int n;
        cin>>n;
        assert(n <= 16384);
        for (int i=1;i<=n;i++) {
            cin>>a[i];
            a[i]+=a[i-1];
        }
        cout<<solve(1,n)<<endl;
    }
    return 0;
}

 Tested by nikasvanidze

Problem Tester's code :

//O(N*ANS)
#include <bits/stdc++.h>
using namespace std;
long long a[1000000];

int sol(int l,int r){
    for (int x=l;x<r;x++)
    if (a[x]*2==a[r]+a[l-1]) return max(sol(l,x),sol(x+1,r))+1;
    return 0;
}

int main() {
    int t;
    cin>>t;
    assert(t<=10);
    while (t--){
        int n;
        cin>>n;
        assert(n<=16384);
        for (int i=1;i<=n;i++) {
            cin>>a[i];
            assert(a[i]<=1000000000ll);
            a[i]+=a[i-1];
        }
        cout<<sol(1,n)<<endl;
    }
    return 0;
}